A teoria dos jogos, um ramo da matemática aplicado amplamente na economia e nas ciências sociais, oferece uma estrutura dominante para entender a tomada de decisões em situações de interdependência. Embora muitas vezes associada a cenários de competição, a teoria dos jogos também fornece insights fundamentais sobre a cooperação.
O dilema que emerge na intersecção entre decisão individual e coletiva é um dos temas centrais dessa teoria, e sua aplicação vai muito além dos jogos de soma zero.
Este artigo explora as bases filosóficas e econômicas por trás da cooperação, destacando como a teoria dos jogos ilumina as complexidades da tomada de decisão colaborativa em uma economia de mercado.
Origens da Teoria dos Jogos: O Equilíbrio entre Competição e Cooperação
A origem da teoria dos jogos remonta ao matemático John von Neumann e ao economista Oskar Morgenstern, que, em 1944, publicaram a obra seminal Theory of Games and Economic Behavior. Essa obra introduziu a ideia de que muitos problemas econômicos e sociais podem ser modelados como jogos nos quais os participantes, ou “jogadores”, devem escolher estratégias racionais, levando em consideração as escolhas dos outros.
Em essência, a teoria dos jogos explora como os indivíduos tomam decisões quando seus resultados dependem das ações de outros.
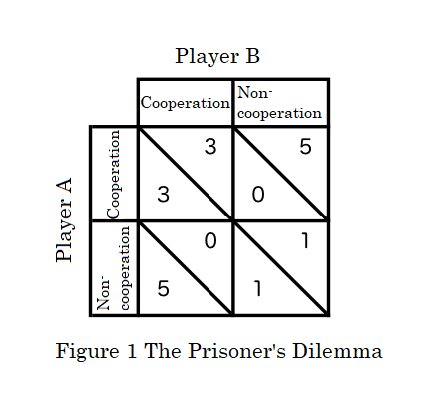
Um dos exemplos mais conhecidos na teoria dos jogos é o Dilema do Prisioneiro, desenvolvido por Merrill Flood e Melvin Dresher nos anos 1950. O dilema apresenta dois prisioneiros acusados de um crime, que devem decidir independentemente entre cooperar um com o outro, permanecendo em silêncio, ou trair o parceiro, confessando o crime.
O dilema do prisioneiro exemplifica o conflito entre o interesse individual e o bem coletivo: a trapaça pode parecer racional do ponto de vista individual, mas, se ambos os jogadores traírem, acabam em uma situação pior do que se tivessem cooperado.
Esse dilema reflete um aspecto crucial da teoria dos jogos: mesmo em um contexto onde os incentivos parecem favorecer a competição, a cooperação pode ser a melhor estratégia a longo prazo. Isso destaca a importância de filosofias que priorizam a colaboração e a construção de confiança mútua entre os jogadores.
Filosofia da Cooperação: De Hobbes a Rousseau
Embora a teoria dos jogos seja uma invenção moderna, as questões filosóficas que ela aborda – o equilíbrio entre interesse próprio e bem coletivo – são tão antigas quanto a filosofia política. Thomas Hobbes, em sua obra Leviatã (1651), descreveu a vida humana no estado de natureza como “solitária, pobre, desagradável, bruta e curta”, onde a competição implacável levava à desordem e à violência.

Para Hobbes, a solução para essa anarquia era a criação de um contrato social, onde os indivíduos renunciavam a parte de sua liberdade em troca de segurança e cooperação sob a autoridade de um governo.
Jean-Jacques Rousseau, por outro lado, ofereceu uma visão mais otimista da cooperação em sua obra O Contrato Social (1762). Rousseau acreditava que os seres humanos, no estado natural, eram naturalmente cooperativos, mas que a civilização e a propriedade privada haviam corrompido esse impulso.
Ele propôs que, por meio de um pacto social justo, os indivíduos poderiam reconciliar seus interesses pessoais com o bem comum, em tese criando uma sociedade mais harmônica.
O conceito de dilema social, que permeia a teoria dos jogos, é uma atualização moderna dessas questões. Filósofos como Hobbes e Rousseau já haviam identificado que a cooperação era essencial para a estabilidade social, mas também frágil, dada a tendência dos indivíduos de agir em função de seus próprios interesses. A teoria dos jogos formaliza essas preocupações ao modelar como a cooperação pode ser incentivada ou prejudicada por estruturas de recompensa e punição.
John Nash e o Equilíbrio de Nash: Uma Perspectiva Colaborativa
Na década de 1950, John Nash, um dos grandes nomes da teoria dos jogos, revolucionou o campo ao desenvolver o conceito de equilíbrio de Nash, uma solução para jogos não cooperativos em que nenhum jogador tem incentivo para mudar sua estratégia unilateralmente.
Embora muitas vezes interpretado como uma formalização da racionalidade individual, o equilíbrio de Nash tem implicações profundas para a cooperação.
Em jogos de soma não zero, onde há potenciais ganhos de colaboração, o equilíbrio de Nash demonstra como os jogadores podem alcançar resultados mutuamente benéficos ao reconhecer a interdependência de suas decisões.
Esse é o cerne da filosofia por trás da cooperação: embora os jogadores possam agir de forma competitiva, a racionalidade mútua frequentemente os leva a escolher estratégias que promovem o interesse comum. Nash mostrou que a cooperação, longe de ser um ideal utópico, pode ser o resultado lógico da busca individual por ganhos.

Jogos Repetidos e a Estratégia do “Tit-for-Tat”

Outro desenvolvimento crucial na teoria dos jogos, com fortes implicações para a cooperação, é o conceito de jogos repetidos. Enquanto no dilema do prisioneiro clássico os jogadores fazem uma única escolha, nos jogos repetidos os jogadores interagem várias vezes. Nesse contexto, a cooperação pode emergir naturalmente como uma estratégia racional.
O psicólogo e matemático Robert Axelrod, em sua obra The Evolution of Cooperation (1984), realizou simulações de jogos repetidos do dilema do prisioneiro e descobriu que a estratégia mais bem-sucedida era o “tit-for-tat” (ou “olho por olho”).
Nesta estratégia, o jogador começa cooperando e, em seguida, espelha a última jogada de seu oponente. Isso significa que, se o oponente cooperar, a cooperação continua; se trair, o jogador responde de maneira recíproca. Axelrod mostrou que, em interações repetidas, a cooperação pode emergir como uma estratégia dominante, mesmo entre jogadores que buscam maximizar seus próprios interesses.
Esse resultado reforça a filosofia de que a confiança e a reciprocidade são essenciais para a cooperação de longo prazo. Ao contrário da visão hobbesiana de que a natureza humana tende ao conflito, os resultados de Axelrod indicam que, em situações de interação contínua, a cooperação não é apenas possível, mas pode ser a estratégia mais eficaz.
Teoria dos Jogos, Economia e Cooperação: Um Caminho para a Prosperidade
No contexto de uma economia de mercado, a cooperação desempenha um papel central na criação de valor e na promoção do bem-estar coletivo. Empresas cooperam em consórcios, investidores colaboram em joint ventures, e mesmo na política econômica internacional, tratados e acordos dependem de estruturas de incentivo que promovem a cooperação entre países.
O conceito de bens públicos e externalidades são exemplos de dilemas econômicos nos quais a cooperação é essencial. Bens públicos, como infraestrutura ou defesa nacional, são indivisíveis e não podem ser fornecidos eficientemente pelo mercado sem alguma forma de cooperação.
Da mesma forma, externalidades, como a poluição, requerem uma solução coletiva, já que a busca pelo interesse individual pode levar a resultados sub-ótimos para a sociedade como um todo.
A teoria dos jogos, ao modelar esses problemas, oferece insights valiosos sobre como as políticas econômicas podem ser desenhadas para incentivar a cooperação, seja por meio de sanções, recompensas ou estruturas legais que alinhem os interesses individuais e coletivos.

A teoria dos jogos e a filosofia da cooperação estão profundamente interligadas. Desde as reflexões filosóficas de Hobbes e Rousseau sobre a necessidade de cooperação para a construção de sociedades justas, até as contribuições matemáticas de John Nash e Robert Axelrod, fica claro que a cooperação não é apenas um ideal moral, mas uma estratégia viável e racional em muitos contextos.
Em uma economia de mercado, onde as interações interdependentes são a norma, entender os mecanismos da cooperação é essencial para promover a prosperidade, evitar conflitos e construir um futuro mais equilibrado.